Stigmergy
[Repost from GeorgieBC under CC-by-nc-sa, translated german version]
Stigmergy is a mechanism of indirect coordination between agents or actions. The principle is that the trace left in the environment by an action stimulates the performance of a next action, by the same or a different agent. In that way, subsequent actions tend to reinforce and build on each other, leading to the spontaneous emergence of coherent, apparently systematic activity. Stigmergy is a form of self-organization. It produces complex, seemingly intelligent structures, without need for any planning, control, or even direct communication between the agents. – Wikipedia
A personality based system can never allow for mass collaboration on a global scale without representation such as that seen in organizations like the United Nations. If the world is to move away from representation and allow all voices to be heard, we need to find methods of collaboration which work with idea and action based systems. Concentric user groups with epistemic communities and knowledge bridges may work for idea based systems; for action, stigmergy may be the best option.
Currently, the typical response to a situation which requires an action is to create a noun, in the form of a committee, commission, organization, corporation, ngo, government body, etc. Far too often, the action never appears at all as the focus is always on the organization and the personalities involved instead.
Most systems are now run by competitive organizations. Competition creates redundancy, is slow and wastes resources on idea protection, advertisement, and more. Competition also requires secrecy which blocks progress and auditing and causes lost opportunities and ideas. Patents and copyrights further limit speed and the potential for mass input of ideas. Collaboration between the people with the greatest expertise does not happen unless they are hired by the same project.
The alternative to competition has traditionally been cooperation. This is most effective only in groups of two to eight people. For groups larger than 25, cooperation is agonizingly slow, an exercise in personality management which quickly degenerates into endless discussion and soothing of ruffled feathers, is extremely vulnerable to agent provocateurs, and in large scale groups very seldom accomplishes anything of value. Cooperation traditionally operates on the democratic principle that all voices are equal, so it does not allow for leaders, or users with greater expertise, energy or understanding to have greater influence than those on the periphery. Cooperation wastes a great deal of time and resources in both discussing and discussing the discussions. In an action based system, this discussion is rarely required as the opinion of those not doing the work is probably of little value unless it is solicited advice from a trusted knowledgeable party.
Cooperation and consensus based systems are usually dominated by extroverted personalities who make decisions to control the work of others and are justly resented by those doing the actual work. Most workers do not enjoy a hierarchical system as shown in the chart below, as they lose autonomy, mastery and creative control over their own work; the feeling at the bottom is no different whether there is a horizontal or a hierarchical structure making the decisions. Cooperative systems frequently use consensus or votes to make decisions for the entire group; these methods may not produce the best results as many people may not understand the work if they are not actually doing it, and they may demand things they would never be willing to do themselves. Consensus based systems are also prone to the ‘hive mind’ appropriation of credit for individual ideas and labour which causes further resentment.
Hierarchical System (click to enlarge)
Consensus Hierarchy (click to enlarge)
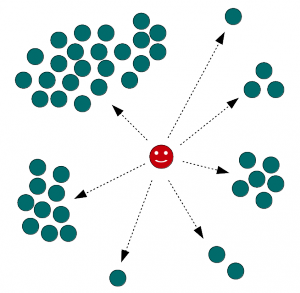
In the Stigmergy chart below, all workers have full autonomy to create as they wish; the power of the user group is in the ability to accept or reject the work. Since there is no officially designated person to perform a task the users are free to create alternatives if they do not like what they are offered. Workers are free to create regardless of acceptance or rejection; in the chart below some work may be accepted by the largest group, some alternatives for a different user group, some only by a small group, and sometimes the worker will be alone with their vision. In all cases the worker is still free to create as they wish. History has shown no drastically innovative ideas that received instant mainstream acceptance and history also shows that radically new ideas are most often the result of solitary vision; to leave control of work to group consensus only is to cripple innovation.
Stigmergy (click to enlarge)
In a competitive environment, a new idea is jealously guarded, legally protected and shrouded in secrecy. Great effort is expended in finding supporters for the idea while also ensuring that the idea remains covered by legal protections such as non-disclosure agreements. The idea remains inextricably bound to the creator until it is legally transferred to another owner and all contributors work for the owner, not the idea. Contributors must then be rewarded by the owner which further limits the potential for development and wastes more resources in legal agreements, lawsuits, etc. Contributors have no interest in whether the project succeeds or fails and no motivation to contribute more than they are rewarded for.
If the idea is instead developed cooperatively, it must first be pitched by the originator, who will attempt to persuade a group to adopt the idea. The group must be in agreement with the idea itself and with every stage of its development. The majority of energy and resources are spent on communication, persuasion, and personality management, and the working environment is fraught with arguments and power struggles. Because the project is driven by a group, albeit a cooperative one, the group is still competitive with other similar outside projects, and still wastes resources and energy on secrecy, competitive evangelizing, etc. Both competitive and cooperative projects will die if the group that runs the project leaves and both will attract or repel contributors based on the personalities of the existing group. Both are hierarchical systems where individuals need to seek permission to contribute. Both focus on the authority of personalities to approve a decision instead of focusing on the idea or action itself.
Stigmergy is neither competitive nor traditionally collaborative.
With stigmergy, an initial idea is freely given, and the project is driven by the idea, not by a personality or group of personalities. No individual needs permission (competitive) or consensus (cooperative) to propose an idea or initiate a project. There is no need to discuss or vote on the idea, if an idea is exciting or necessary it will attract interest. The interest attracted will be from people actively involved in the system and willing to put effort into carrying the project further, not empty votes from people with little interest or involvement. Since the project is supported or rejected based on contributed effort, not empty votes, input from people with more commitment to the idea will have greater weight. Stigmergy also puts individuals in control over their own work, they do not need group permission to tell them what system to work on or what part to contribute.
The person with the initial idea may or may not carry the task further. Evangelizing the idea is voluntary, by a group that is excited by the idea; they may or may not be the ones to carry it out. It is unnecessary to seek start up funding and supporters; if an idea is good it will receive the support required. (In practice, that is not true yet, as few people have the free time to put into volunteer projects because most are tied to compulsory work under the existing financial system. Additionally, we still live in a personality driven system where only powerful personalities are heard.) Secrecy and competition is unnecessary because once an idea is given, it and all new development belongs to anyone who chooses to work on it. Anyone can submit work for approval, the idea cannot die or be put on hold by personalities; acceptance or rejection is for the work contributed, not the person contributing it. All ideas are accepted or rejected based on the needs of the system.
Responsibility and rights for the system rest with the entire user group, not just the creators. There is no need for people to leave the system based on personality conflicts as there is no need for communication outside of task completion and there are usually plenty of jobs with complete autonomy. As no one owns the system, there is no need for a competing group to be started to change ownership to a different group.
Stigmergy provides little scope for agent provocateurs as only the needs of the system are considered. Anyone working against the system’s functionality is much easier to see and prevent than someone blocking progress with endless discussion and creation of personality conflicts. Because the system is owned by all, there is also no one leader to target.
Nodes
As work progresses and core team and members grow, more interested and dedicated personalities emerge which begin to steer direction. Specialties are formed around the core team’s interests as the core team produces the most work and the work most valued by the rest of the user group. Systems beyond a certain level of complexity begin to lack coherence as the group’s energy and focus moves from broad to narrow, following the interests of the core team and the availability of resources; parts of the original system may be left undone.
As more members are added, more will experience frustration at limited usefulness or autonomy. Some of these members will have an interest in the work left undone and they will create a new node of like minded members and new people to take care of the undone work. Alternatively, casual users and observers of the system, who lack the desire or expertise to be a more active part of the original system, will see a different need created and start a new node. Rather than the traditional corporate model of endless acquisition and expansion, stigmergy encourages splintering into different nodes. Because each individual is responsible only for their own work, and no one can direct a group of workers, expansion means more work for the individual, a self limiting prospect. As a system grows, the additional work requires either additional resources or splintering; as communication is easier and there is more autonomy in smaller groups, splintering is the more likely outcome of growth.
Communication between nodes of a system is on an as needed basis. Transparency allows information to travel freely between the various nodes, but a formal relationship or communication method is neither necessary nor desirable. Information sharing is driven by the information, not personal relationships. If data is relevant to several nodes it will be immediately transmitted to all, no formal meetings between official personalities are necessary.
Any node can disappear without affecting the network, and the remaining necessary functionality of that node can be taken up by others. Nodes which find they are performing the same tasks will likely join, or one will be rendered obsolete by lack of use. New nodes are only created to fulfill a new need or provide greater functionality; it is inefficient to have the same task performed twice, and that only occurs if a second group discovers an alternative method that the first group is unwilling to adopt. In that case, the best system will win the most support from the user group, the other will die or remain as a valued alternative. Any user can contribute to the node which best matches their interests and abilities, or contribute to multiple nodes.
The future
A new system of governance or collaboration that does not follow a competitive hierarchical model will need to employ stigmergy in most of its action based systems. It is neither reasonable nor desirable for individual thought and action to be subjugated to group consensus in matters which do not affect the group, and it is frankly impossible to accomplish complex tasks if every decision must be presented for approval; that is the biggest weakness of the hierarchical model. The incredible success of so many internet projects are the result of stigmergy, not cooperation, and it is stigmergy that will help us build quickly, efficiently and produce results far better than any of us can foresee at the outset.


Stigmergy is an interesting model to me, but as you write, it is „not true yet“ that it would work like that in our present society. Something like a basic income is absolutely necessary to set people free to act and choose what they like.
While reading I had one big question: what exactly is „the system“ you are talking about? It isn’t defined anywhere in the text.
@Timo Ollech: The question should go to the original author. I suppose »system« is not meant in a distinct sense, but rather as a general placeholder.
Here’s the answer to the systems question from the author: »This article is part of a series: ‘Governance and other systems of mass collaboration’. Systems are discussed in ‘Governance by user groups’ “User groups are seldom simply entire nations and there are users of differing levels of involvement in each system. International systems would include things such as the internet, telecommunications and knowledge, local systems would include things such as transit, food production and social services”. ‘System’ as I use it is really the same as the word definition. Usually in governance systems are divided into ministries, departments, etc.«